D1. Range Sorting (Easy Version)(单调栈+思维)
...大约 2 分钟
题目
题意
- 给一个整数n和一个数组a[1~n]
- 一次次排序操作的代价是,r - l
- 求把所有子数组,排成有序的最小代价和
思路
easy版本可以用O()的算法,我们可以枚举左右端点
假设一段的最优排序方法如图
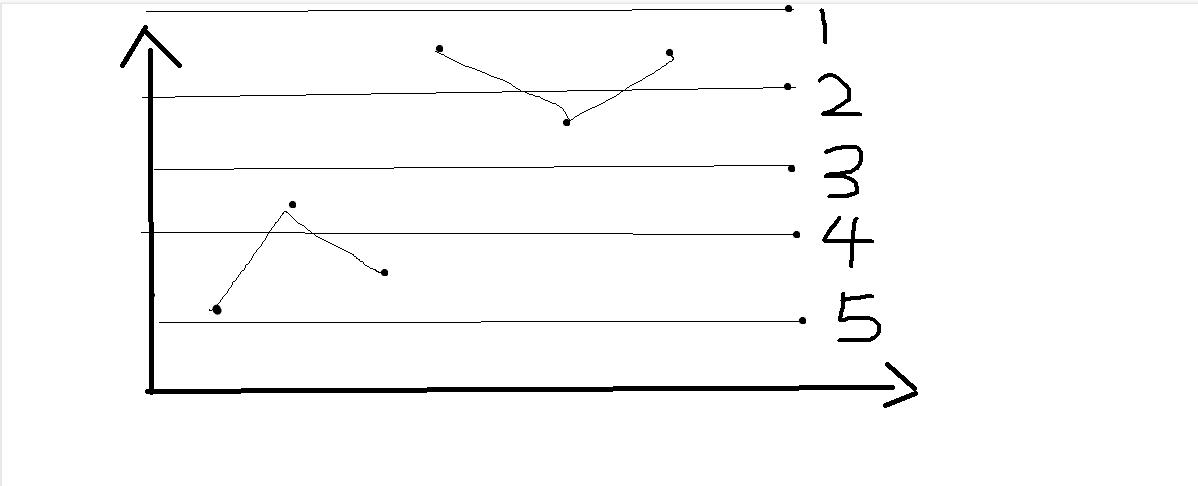
任意长度的一段序列排序可能是排序多个子序列
所以我们需要讨论加上一个点的情况
- 一号点比之前所有点大,所以不需要排序
- 二号点在第二段中间,所以需要和第二段放在一起排序,代价+1
- 三号点和第二段一起排序,代价+1,同上一情况
- 观察可以发现,把四号点排序需要和第一段和第二段一起排序,相当于合并了这两个段,代价合并段的长度+1
- 同上一步情况
讨论出了所有的情况,就可以发现这个思路类似单调栈
找到第一个段上最大值小于当前添加值的段,然后合并(弹出后操作,再返回栈中)
但是需要注意的是,这个单调栈维护的是一个段的信息,即段中的最大值
所以在栈中放入,每个段中的最大值,还要用已有的最大值来更新,之后放入的最大值
代码
int a[N];
int n;
void solve()
{
cin >> n;
for(int i = 1;i <= n;i ++)cin >> a[i];
int ans = 0;
for(int i = 1;i <= n;i ++)
{
stack<int> sta;
for(int j = i;j <= n;j ++)
{
int cur = a[j];
while(sta.size() && sta.top() > a[j])
{
cur = max(cur,sta.top());
sta.pop();
}
sta.push(cur);
ans += j - i + 1 - sta.size();
}
}
cout << ans << endl;
}
Powered by Waline v2.15.5