讲课:拓扑排序、最短路算法
...大约 3 分钟
什么是图?

把图在计算机中表示(储存)

拓扑排序
度
- 与一个顶点 v 关联的边的条数称作该顶点的 度 (degree)
- 在有向图 G = (V, E) 中,以一个顶点 v 为起点的边的条数称为该顶点的 出度 (out-degree),
- 以一个顶点 v 为终点的边的条数称为该节点的 入度 (in-degree)
思路
首先记录各个点的入度
然后将入度为 0 的点放入队列
将队列里的点依次出队列,然后找出所有出队列这个点发出的边,删除边,同事边的另一侧的点的入度 -1。
如果所有点都进过队列,则可以拓扑排序,输出所有顶点。否则输出-1,代表不可以进行拓扑排序。
参考代码

应用
判断图中是否有环路
练习
最短路算法
dijkstra单源最短路算法和堆优化
思路
核心思想是利用贪心策略,从源点开始,逐步向外扩展最短路径,直到扩展到目标点为止。
Dijkstra算法维护当前已知的最短路径和距离源点最近的节点,然后根据贪心策略选择最优节点进行扩展。
初始化dist数组,将源点到其他各个顶点的距离全部设为无穷大。将源点标记为已确定最短距离的顶点。
遍历与源点相邻的所有顶点,更新它们的距离,即若源点到该相邻顶点的距离小于目前dist数组中保存的距离,则将该距离更新为更小的值。
从尚未确定最短距离的顶点中选择一个与源点距离最小的顶点,将其标记为已确定最短距离的顶点,并继续遍历其相邻顶点。
重复上面两个步骤,直到所有顶点的最短距离都已被确定。
dijkstra
练习
bellman-ford 算法和SPFA优化
- bellman-ford 算法的松弛操作
- 枚举所有边,松弛所有点到原点的距离
- 跑正常的有最短路的图没问题(最短路径存在,并且显然不超过点的数量-1)
- 但存在负环时,可以知道途中不存在最短路,因为每次松弛都会把最短路变得越来越小,没有意义
- 一般来说,一个图存在负环,就不可能有最短路,所以用处不多,最多用来判断是否存在负环
- spfa只有上一次被松弛的结点,所连接的边,才有可能引起下一次的松弛操作。

folyd 多源最短路
借助中间点来设计最短路算法
- 定义一个数组 f[k][x][y],表示只允许经过结点 1 到 k,结点 x 到结点 y 的最短路长度。
- f[0][x][y]:x 与 y 的边权,或者 0,或者 无穷
- f[k][x][y] = min(f[k-1][x][y], f[k-1][x][k]+f[k-1][k][y])(f[k-1][x][y],为不经过 k 点的最短路径,而 f[k-1][x][k]+f[k-1][k][y],为经过了 k 点的最短路)。
核心代码

因为第一维对结果无影响,我们可以发现数组的第一维是可以省略的,于是可以直接改成 f[x][y] = min(f[x][y], f[x][k]+f[k][y])。
总结
图的概念和表示方法
- G = (V,E) 意思是 Graph = (Vertices,Edges),图 = (点集,边集)
- 图有无向图、有向图、混合图,有带权图、无权图……树是图的一种
- 图的表示的方法有:邻接矩阵、邻接表、链式向前星
拓扑排序
- 理解度的含义
- 然后将入度为 0 的点放入队列,删边,更新度数,再次入队
- 可以用来找环路
最短路
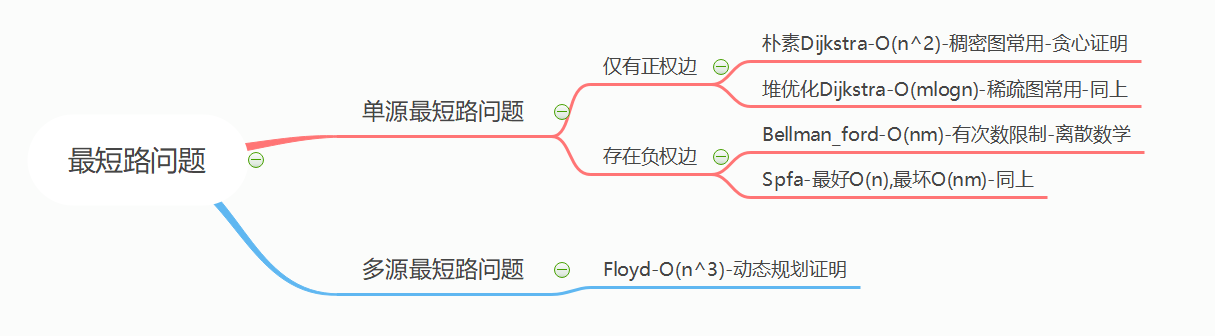

参考资料:
Powered by Waline v2.15.5